1.6 Предел последовательности событий.

Определение 1.16: Множество $A^*$ тех и только тех элементов, которые содержаться в бесконечном числе элементов последовательности $\{A_n\}$, называется верхним пределом последовательности $\{A_n\}$, при этом обозначают $$A^*=\lim_{n\to\infty}\sup_{k>n}A_k=\varlimsup_{n\to\infty}A_n.$$

Теорема 1.2: $A^*=\bigcap_{n=1}^\infty\bigcup_{k=n}^{\infty}A_k.$

Доказательство: $\forall{n}\in\mathbb{N}\,\exists{k}>n:\omega\in{A}_k\Leftrightarrow\omega\in\bigcap_{n=1}^\infty\bigcup_{k=n}^\infty{A}_k.$

Определение 1.17: Множество $A_*$ тех и только тех элементов, которые содержаться во всех элементах последовательности $\{A_n\}$ за исключением некоторого конечного их числа, называется нижним пределом последовательности $\{A_n\}$, при этом обозначают $$A_*=\lim_{n\to\infty}\inf_{k>n}A_k=\varliminf_{n\to\infty}A_n.$$
Очевидно, что $A_*\subset{A}^*$.

Теорема 1.3: $A_*=\bigcup_{n=1}^\infty\bigcap_{k=n}^\infty{A}_k.$

Доказательство: Если $\omega\in{A}_*$, то существует максимальное $m\in\mathbb{N}$ такое, что $\omega\notin{A}_m$, то есть $\omega\in\bigcap_{k=m+1}^\infty{A}_k$.
С другой стороны, $$\omega\in\bigcup_{n=1}^\infty\bigcap_{k=n}^\infty{A}_k\Rightarrow\exists{m}\in\mathbb{N}:\omega\in\bigcap_{k=m}^\infty{A}_k\Rightarrow\forall{k}\in\mathbb{N}(k>m\Rightarrow\omega\in{A}_k),$$ то есть число элементов, которым $\omega$ не принадлежит конечно и не превосходит $m$.

Определение 1.18: Говорят, что последовательность $\{A_n\}$ сходится если $$A:=\varliminf_{n\to\infty}A_n=\varlimsup_{n\to\infty}A_n,$$ при этом число $A$ называют пределом последовательности $\{A_n\}$ и обозначают $\lim_{n\to\infty}A_n=A$.

Теорема 1.4: Если для любого $n\in\mathbb{N}$ $A_{n+1}\subset{A}_n$, то последовательность $\{A_n\}$ сходящаяся и $\lim_{n\to\infty}A_n=\bigcap_{n=1}^\infty{A}_n$.

Доказательство: $$\bigcup_{k=n}^\infty{A}_k=A_n\Rightarrow{A}^*=\bigcap_{n=1}^\infty\bigcup_{k=n}^\infty{A}_k=\bigcap_{n=1}^\infty{A}_n.$$ $$\bigcap_{k=n}^\infty{A}_k=\bigcap_{n=1}^\infty{A}_n\Rightarrow{A}_*=\bigcup_{n=1}^\infty\bigcap_{k=n}^\infty{A}_k=\bigcup_{n=1}^\infty\bigcap_{n=1}^\infty{A}_n=\bigcap_{n=1}^\infty{A}_n.$$ Аналогично показывается, что в любая неубывающая последовательность $\{A_n\}$ сходится и $\lim_{n\to\infty}A_n=\bigcup_{n=1}^\infty{A}_n$.

1.7 Теорема о непрерывности вероятностной меры.

Пример 1.10: Приведем пример аддитивной, но не счетно аддитивной вероятностной меры.
Пусть $\Omega=\mathbb{Q}\cap[0,1]$. Для любых $a,b\in\Omega$ обозначим $A_{a,b}:=[a,b]\cap\Omega$. Положим $\mathfrak{A}$ - все счетные объединения множеств вида $A_{a,b}$. Пусть функция $P:\mathfrak{A}\to[0,1]$ такая, что $P(A_{a,b})=b-a$, для любой конечной совокупности попарно непересекающихся множеств вида $A_{a,b}$ положим $$P\left(\bigcup_{k=1}^nA_{a_k,b_k}\right)=\sum_{k=1}^nP(A_{a_k,b_k}).$$ То есть вероятностная мера $P$ конечно аддитивна. Однако, для любого ${r\in\Omega}$ $\{r\}=[r,r]=A_{r,r}\in\mathfrak{A}$, $P(A_{r,r})=r-r=0$, следовательно, $$\sum_{r\in\Omega}P(A_{r,r})=0\neq1=P(\Omega)={P}\left(\bigcup_{r\in\Omega}A_{r,r}\right).$$ То есть функция $P$ конечно, но не счетно аддитивна. В следующей теореме формулируются условия, при которых из конечной аддитивности вероятностной меры следует её счетная аддитивность.

Теорема 1.5: Пусть $P$ - конечно аддитивная мера на измеримом пространстве $(\Omega,\mathfrak{A})$, тогда следующие утверждения эквивалентны

1. $P$ - счетно аддитивная мера на $(\Omega,\mathfrak{A})$,
2. Для любой неубывающей последовательности $\{A_n\}$ из $\mathfrak{A}$ $$P(\lim_{n\to\infty}A_n)=P\left(\bigcup_{n=1}^\infty{A}_n\right)=\lim_{n\to\infty}P(A_n).$$
3. Для любой невозрастающей последовательности $\{A_n\}$ из $\mathfrak{A}$ $$P(\lim_{n\to\infty}A_n)=P\left(\bigcap_{n=1}^\infty{A}_n\right)=\lim_{n\to\infty}P(A_n).$$
4. Для любой невозрастающей последовательности $\{A_n\}$ из $\mathfrak{A}$ $$\bigcap_{n=1}^\infty{A}_n=\varnothing\Rightarrow\lim_{n\to\infty}P(A_n)=0$$

Доказательство:
$1)\Rightarrow2)$ Положим $B_1:=A_1$ и для любого $k>1$ ${B_k:=A_k\backslash{A}_{k-1}}$. Так как для любого $i\in\mathbb{N}$ $A_i\subset{A}_{i+1}$, то для любых неравных $t,s\in\mathbb{N}$ $B_tB_s=\varnothing$ и для любого $n\in\mathbb{N}$ $A_n=\bigcup_{k=1}^nB_k$. Тогда, $\bigcup_{k=1}^\infty{A}_k=\bigcup_{k=1}^\infty{B}_k$ и по аддитивности $P$ $P(A_n)=\sum_{k=1}^nP(B_k)$. Следовательно, так как $P$ счетно аддитивна $$ P(\lim_{n\to\infty}A_n)=P\left(\bigcup_{k=1}^\infty{A}_k\right)=P\left(\bigcup_{k=1}^\infty{B}_k\right)= \sum_{k=1}^\infty{P}(B_k)=\lim_{n\to\infty}\sum_{k=1}^nP(B_k)=\lim_{n\to\infty}P(A_n). $$
$2)\Rightarrow3)$ Для любого $n\in\mathbb{N}$ $\overline{A}_n:=\Omega\backslash{A}_n$, тогда для любого $n\in\mathbb{N}$ $\overline{A}_n\subset\overline{A}_{n+1}$. Следовательно, по п. 2 $$ P\left(\bigcap_{n=1}^\infty{A}_n\right)=1-P\left(\overline{\bigcap_{n=1}^\infty{A}_n}\right)=1-P\left(\bigcup_{n=1}^\infty\overline{A}_n\right)= 1-\lim_{n\to\infty}P(\overline{A}_n)=\lim_{n\to\infty}(1-P(\overline{A}_n))=\lim_{n\to\infty}P(A_n) $$
$3)\Rightarrow4)$ По п. 3 $$\lim_{n\to\infty}P(A_n)=P\left(\bigcap_{n=1}^\infty{A}_n\right)=P(\varnothing)=0.$$
$4)\Rightarrow1)$ Фиксируем последовательность попарно не пересекающихся множетсв $\{A_n\}$ из $\mathfrak{A}$. Необходимо доказать, что $$P\left(\bigcup_{n=1}^\infty{A}_n\right)=\sum_{n=1}^\infty{P}(A_n).$$ Для любого $n\in\mathbb{N}$ обозначим $C_n:=\bigcup_{k=n+1}^\infty{A}_n$, тогда для любого $n\in\mathbb{N}$ $C_{n+1}\subset{C}_n$ и, следовательно, по теореме 1.4 $\lim_{n\to\infty}C_n=\bigcap_{n=1}^\infty{C}_n$. Докажем от противного, что $\bigcap_{n=1}^\infty{C}_n=\varnothing$. Предположим, что существует $\omega\in\bigcap_{n=1}^\infty{C}_n$, тогда $$ \exists{n}\in\mathbb{N}:\forall{k}\geq{n}(\omega\in{C}_k)\Rightarrow\omega\in\bigcup_{k=n+1}^\infty{A}_n\Rightarrow \exists{k}_0>n:\omega\in{A}_{k_0}\wedge\omega\in{C}_{k_0}=\bigcup_{k=k_0+1}^\infty{A}_k\Rightarrow \exists{k}_1>k_0:\omega\in{A}_{k_1}A_{k_0}\Rightarrow{A}_{k_1}A_{k_0}\neq\varnothing. $$ Последнее неравенство невозможно так как элементы последовательности $\{A_n\}$ попарно не пересекаются по условию. Таким образом доказано, что $\lim_{n\to\infty}{C}_n=\bigcap_{n=1}^\infty{C}_n=\varnothing$. Тогда из п. 4 следует, что $\lim_{n\to\infty}P(C_n)=0$, при этом по аддитивности меры $P$ $$ \bigcup_{n=1}^\infty{A}_n=\left(\bigcup_{k=1}^n{A}_n\right)\cup{C}_n\Rightarrow {P}\left(\bigcup_{n=1}^\infty{A}_n\right)=P\left(\bigcup_{k=1}^n{A}_k\right)+P(C_n)=\sum_{k=1}^n{P}(A_k)+P(C_n). $$ Переходя к пределу при $n\to\infty$ получим $$P\left(\bigcup_{n=1}^\infty{A}_n\right)=\lim_{n\to\infty}\sum_{k=1}^n{P}(A_k)+\lim_{n\to\infty}P(C_n)=\sum_{n=1}^\infty{P}(A_n).$$

Теорема 1.6: Теорема Каратеодори.
Пусть $\mathfrak{A}$ - алгебра подмножеств $\Omega$, $\sigma(\mathfrak{A})$ - минимальная $\sigma$-алгебра содержащая $\mathfrak{A}$, $P$ - $\sigma$-аддитивная вероятностная мера на $\mathfrak{A}$, тогда существует единственная $\sigma$-аддитивная вероятностная мера заданная на $\sigma(\mathfrak{A})$, которая является продолжением меры $P$.

Доказательство:
Доказательство, например, в Ширяев А. Н. 2004 г. "Вероятность - 1" стр. 192.

1.8 Условные вероятности.

Определение 1.19: Пусть $(\Omega,\mathfrak{A},P)$ - вероятностное пространство. Тогда для любых $A\in\mathfrak{A}$, $B\in\mathfrak{A}\backslash{\varnothing}$ число $P_B(A):=P(A/B):=\frac{P(AB)}{P(B)}$ называется условной вероятностью события $A$ при условии, что событие $B$ произошло.

Пример 1.11: Пусть $\Omega=\{\omega_1,\ldots,\omega_N\}$, $\mathfrak{A}:=\mathcal{P}(\Omega)$, для любого $A\in\mathfrak{A}$ $P(A):=\frac{|A|}{|\Omega|}$, тогда $(\Omega,\mathfrak{A},P)$ - вероятностное пространство (классическая схема).
Тогда $$P(A/B)=\frac{P(AB)}{P(B)}=\frac{|AB|/{N}}{|B|/{N}}=\frac{|AB|}{|B|}.$$

Если $(\Omega,\mathfrak{A},P)$ - вероятностное пространство, $P(B)>0$, то

1. $\mathfrak{A}_B:=\{A\cap{B}\mid{A}\in\mathfrak{A}\}$ - алгебра.
2. $\forall{A}\in\mathfrak{A}_B$ $P_B(A)\geq0$
3. $P_B(B)=1$
4. Для любых несовместных $A,C\in\mathfrak{A}$ $$P_B(A\cup{C})=\frac{P((A\cup{C})B)}{P(B)}=\frac{P(AB)+P(CB)}{P(B)}=P_B(A)+P_B(C).$$

Теорема 1.7: Теоерма об умножении вероятностей.
Пусть $A_1,\ldots,A_n\in\mathfrak{A}$ такие, что $P(A_1\cdots{A}_n)>0$, тогда $$P(A_1\cdots{A}_n)=P(A_1)P(A_2/{A_1})P(A_3/{A}_1A_2)\cdots{P}(A_n/{A}_1\cdots{A}_{n-1}).$$

Доказательство:
Докажем индукцией по $n$.

1. Так как $A_1A_2\subset{A_1}$, то $P(A_1)\geq{P}(A_1A_2)>0$, поэтому при $n=2$ утверждение следует из определения условной вероятности.
2. Пусть утверждение верно при $k=n-1$.
   Так как $P(A_1\cdots{A}_{n-1})\geq{P}(A_1\cdots{A}_n)>0$ то по определению условной вероятности $$P(A_1\cdots{A}_n)=P(A_1\cdots{A}_{n-1})P(A_n/{A_1}\cdots{A}_{n-1})$$ и утверждение следует из предположения индукции.

Определение 1.20: События $A,B\in\mathfrak{A}$ называются независимыми, если $P(AB)=P(A)P(B)$.

Если независимые события $A,B\in\mathfrak{A}$ такие, что $P(A)\neq0$, $P(B)\neq0$, то $$P(A)P(B)=P(AB)=P(A)P(B/A)=P(B)P(A/B).$$

Определение 1.21: События $A_1,\ldots,A_n\in\mathfrak{A}$ называются попарнонезависимыми, если для любых неравных $i,j\in\overline{1,n}$ события $A_i$, $A_j$ независимы.

Определение 1.22: События $A_1,\ldots,A_n\in\mathfrak{A}$ называются независимыми в совокупности, если $$\forall{k}\in\overline{2,n}\,\forall{i_1,\ldots,i_k}\in\overline{1,n}(P(A_{i_1}\cdots{A}_{i_k})=P(A_{i_1})\cdots{P}(A_{i_k})).$$

Если события $A_1,\ldots,A_n$ незвисимы в совокупности, то они попарно независимы, обратное в общем случае неверно.

Пример 1.12: Бернштейн.
Рассмотрим тетраэдр три грани, которого раскрашены соответственно в синий, красны и белый цвета, а четвертая разделена на три части красную, синюю и белую. Грани тетраэдра пронумерованы числами от 1 до 4. Случайный эксперемент заключается в подбрасывании тетраэдра. Элементарным событием будем считать номер грани, на которую упал тетраэдр. Таким образом $\Omega=\{1,2,3,4\}$, $\mathfrak{A}:=\mathcal{P}(\Omega)$, для любого $A\in\mathfrak{A}$ $P(A)=\frac{|A|}{4}$. Рассмотрим события

• $A=\{$На выпавшей грани присутствует красный цвет.$\}$
• $B=\{$На выпавшей грани присутствует синий цвет.$\}$
• $C=\{$На выпавшей грани присутствует белый цвет.$\}$

Определение 1.23: События $H_1,\ldots,H_n\in\mathfrak{A}$ образуют полную группу событий или разбиение, если

1. $\bigcup_{k=1}^n{H}_k=\Omega$,
2. для любых неравных $i,j\in\overline{1,n}$ $H_iH_j=\varnothing$

Теорема 1.8: Формула полной вероятности.
Пусть $H_1,\ldots,H_n$ - полная группа событий, для любого $k\in\overline{1,n}$ $P(H_k)>0$, тогда для любого $A\in\mathfrak{A}$ $$P(A)=\sum_{k=1}^nP(H_k)P(A/H_k)$$

Доказательство:
Так как $$A=A\cap\Omega=A\cap\left(\bigcup_{k=1}^nH_k\right)=\bigcup_{k=1}^nAH_k,$$ и для любых неравных $i,j\in\overline{1,n}$ $AH_i\cap{A}H_j=\varnothing$, то $$P(A)=\sum_{k=1}^nP(AH_k)=\sum_{k=1}^nP(H_k)P(A/H_k).$$

Теорема бывает полезна в тех случаях, когда вычислить условные вероятности проще чем безусловные.

Пример 1.13: Пусть имеется две монеты одинакогого внешнего вида одна симметричная другая с вероятностью выпадения герба $\frac13$. Случайным эксперементом является выбор одной из монет и подбрасывание ее. Рассмотрим события

• $A$ - выпал герб,
• $H_1$ - выбрана симметричная монета,
• $H_2$ - выбрана несимметричная монета.

Пример 1.14: Пусть имеется $n$ экзаменационных билетов, из которых $m$ - лёгкие. Рассмотрим события

• $A_1$ - первому студенту достался лёгкий билет,
• $A_2$ - второму студенту достался лёгкий билет.
• ...

Теорема 1.9: Формула Байеса.
Пусть $H_1,\ldots,H_n$ - полная группа событий, для любого $k\in\overline{1,n}$ $P(H_k)>0$, $A\in\mathfrak{A}$ $P(A)>0$, тогда $$P(H_k/A)=\frac{P(H_k)P(A/H_k)}{\sum_{k=1}^nP(H_k)P(A/H_k)}$$

Доказательство:
По определению условной вероятности и формуле полной вероятности $$P(H_k/A)=\frac{P(AH_k)}{P(A)}=\frac{P(H_k)P(A/H_k)}{P(A)}=\frac{P(H_k)P(A/H_k)}{\sum_{k=1}^nP(H_k)P(A/H_k)}.$$

Пример 1.15: В условиях примера 1.13 вычислим вероятность того, что была выбрана симметричная монета при условии, что выпал герб $$P(H_1/A)=\frac{P(H_1)P(A/H_1)}{P(H_1)P(A/H_1)+P(H_2)P(A/H_2)}=\frac{\frac12\cdot\frac12}{\frac12\cdot\frac12+\frac12\cdot\frac13}=\frac35,$$ и вероятность того, что была выбрана несимметричная монета при условии, что выпал герб $$P(H_2/A)=\frac{P(H_2)P(A/H_2)}{P(H_1)P(A/H_1)+P(H_2)P(A/H_2)}=\frac{\frac12\cdot\frac13}{\frac12\cdot\frac12+\frac12\cdot\frac13}=\frac25,$$

1.8 Условные вероятности.

Пример 1.16: Два человека договорились встретится в промежутке времени от 0 до 1 часа. Каждый из них приходит на место встречи в этот промежуток времени и ждет 10 минут или до конца промежутка. Найдем вероятность того, что встреча состоялась?
Обозначим время прихода первого человека - $x$, время прихода второго - $y$. В качестве меры $\mu$ возьмем площадь. В качестве $\Omega$ возьмем квадрат со стороной 60 $\Omega:=\{(x,y)\mid0\leq{x}<1,0\leq{y}<1\}$, тогда множество $A$ исходов, при которых встреча состоится есть фигура закрашенная серым цветом, то есть $|x-y|<10$.

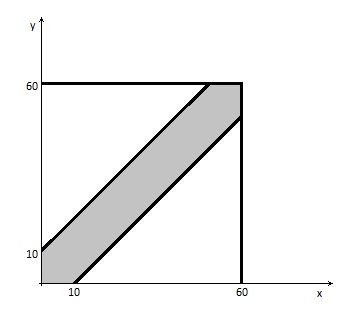
Таким образом $$P(A)=\frac{\mu(A)}{\mu(\Omega)}=\frac{60\cdot60-50\cdot50}{60\cdot60}=\frac{11}{36}$$

Пример 1.17: Задача Бюффона.
Лист бумаги разлинован горизонтальными линиями, расстояние между линиями $2a$. На этот лист случайным образом бросается игла длиной $2L$ $L<a$. Какова вероятность того, что игла пересечет одну из линий?


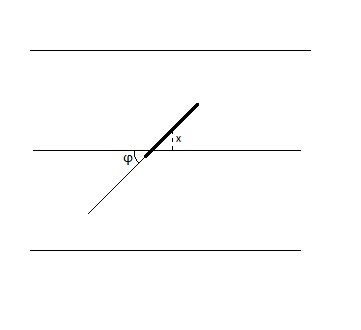
Обозначим $x$ - расстояние от центра иглы до ближайшей линии, $\varphi$ - угол между иглой и горизонталью. В качестве пространства элементарных событий возьмем $\Omega:=\{(x,\varphi)\mid0\leq{x}<a,0\leq\varphi\pi\}$. Таким образом, множество благоприятных исходов это фигура закрашенная серым цветом $A=\{(x,\varphi)\mid{x}<L\sin{\varphi}\}\cap\Omega$.

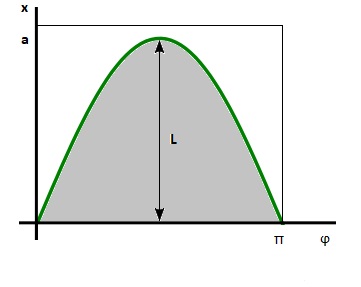
Таким образом, $$\mu(A)=\int\limits_0^\pi L\sin{\varphi}d\varphi=2L\Rightarrow{P}(A)=\frac{\mu(A)}{\mu(\Omega)}=\frac{2L}{a\pi}.$$

previous contents next